Week 01 – Whole Numbers: Binary Number System, Translation Of Word Problems
Whole Numbers
Whole Numbers are simply the numbers 0, 1, 2, 3, 4, 5, … (and so on)
Whole Numbers
Whole Numbers are simply the numbers 0, 1, 2, 3, 4, 5, … (and so on)
No Fractions!
Examples: 0, 7, 212 and 1023 are all whole numbers
(But numbers like ½, 1.1 and 3.5 are not whole numbers.)
Counting Numbers
Counting Numbers are Whole Numbers, but without the zero. Because you can’t “count” zero.
So they are 1, 2, 3, 4, 5, … (and so on).
Natural Numbers
“Natural Numbers” can mean either “Counting Numbers” {1, 2, 3, …}, or “Whole Numbers” {0, 1, 2, 3, …}, depending on the subject.
Integers
Integers are like whole numbers, but they also include negative numbers … but still no fractions allowed!
So, integers can be negative {−1, −2,−3, −4, … }, positive {1, 2, 3, 4, … }, or zero {0}
We can put that all together like this:
Integers = { …, −4, −3, −2, −1, 0, 1, 2, 3, 4, … }
No Fractions!
What is Binary?
Binary is a number system that only uses two digits: 1 and 0. All information that is processed by a computer is in the form of a sequence of 1s and 0s. Therefore, all data that we want a computer to process needs to be converted into binary.

The binary system is known as a ‘base 2’ system. This is because:
- there are only two digits to select from (1 and 0)
- when using the binary system, data is converted using the power of two.
Converting from binary to denary
Understanding denary
People use the denary (or decimal) number system in their day-to-day lives. This system has 10 digits that we can use: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
The value of each place value is calculated by multiplying by 10 (ie by the power of 10). The first few place values look like this:
| Thousands | Hundreds | Tens | Units |
|---|---|---|---|
| (1000s) | (100s) | (10s) | (1s) |
Working out the value of 1024
| Thousands (1000s) | Hundreds (100s) | Tens (10s) | Units (1s) |
| 1 | 0 | 2 | 4 |
| 1 × 1000 + | 0 × 100 + | 2 × 10 + | 4 × 1 |
Converting from binary to denary
To convert a binary number to denary, start by writing out the binary place values. In denary, the place values are 1, 10, 100, 1000, etc – each place value is 10 times bigger than the last. In binary, each place value is 2 times bigger than the last (ie increased by the power of 2). The first few binary place values look like this:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
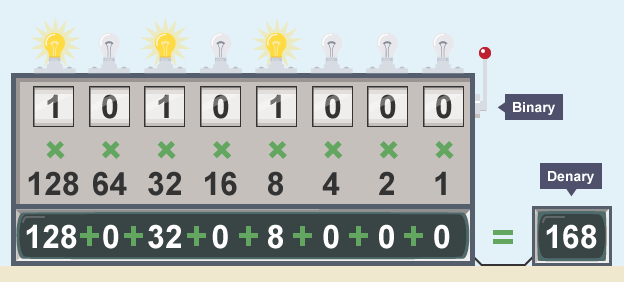
Working out the value of 1010 1000:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1×128 + | 0×64 + | 1×32 + | 0×16 + | 1×8 + | 0×4 + | 0×2 + | 0×1 |
| 128 + | 0 + | 32 + | 0 + | 8 + | 0 + | 0 + | 0 |
So 1010 1000 in binary is equal to 168 in denary.
Converting from Denary to Binary
A method of converting a denary number to binary
This method of converting denary numbers to binary is to use binary place values.
- The first thing to do is write the place values in their columns.
- Then take your denary number, in this case, 84.
- Find the largest place value number that fits into 84 – in this case 64 – then subtract.
- Put a one below and take the remaining 20 to the next column.
- 32 doesn’t fit into 20 so put a ‘0’ in that column.
- 16 fits into 20 leaving 4, so there’s another ‘1’ and move again.
- 8 doesn’t fit into 4, but 4 does, so put a ‘0’ and a ‘1’.
- You have nothing left so zeroes go beneath ‘2’ and ‘1’.
- And there’s your binary number!
There is a very simple method to convert a denary number into a binary number. Let’s take the number 199.
Start by writing out the first few binary place values (128, 64, 32, 16, 8, 4, 2, 1).
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Start at the far left point and say “Can 128 be taken away from 199?”. If it can, do that.
199 – 128 = 71. Because 128 could be taken off, put a 1 in the ‘128’ place value column:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 |
Now repeat for 64: 71 – 64 = 7
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 |
And again for 32: 7 – 32 won’t work, so put a 0 in that place value column.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 |
Try again for 16: 7 – 16 won’t work, so add a 0 to that place value column.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 |
Next is 8: 7 – 8 won’t work. Add a 0 to the ‘8’ place value column.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 |
Try again for 4: 7 – 4 = 3, so add a 1 to the ‘4’ place value column.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Next try 2: 3 – 2 = 1, so add a 1 to the ‘2’ place value column.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
And finally, 1: 1 – 1 = 0 – add a 1 to the ‘1’ place value column.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
This means that 199 as a binary number is 1100 0111.
Note that binary numbers are usually written in blocks of four, separated by a space (eg 0111 1011). In denary, numbers are often written in blocks of three (eg 6 428 721).
A quick way to check whether your binary number is likely to be correct is by looking at the last digit. If the denary number was odd, this last binary digit should be a 1. If it was an even number this binary digit should be a 0.
Adding Binary
When two numbers are added together in denary, we take the first number, add the second number to it and get an answer. For example, 1 + 2 = 3.
When we add two binary numbers together the process is different.
There are four rules that need to be followed when adding two binary numbers. These are:
- 0 + 0 = 0
- 1 + 0 = 1
- 1 + 1 = 10 (binary for 2)
- 1 + 1 + 1 = 11 (binary for 3)
Example
Let’s try adding together two binary numbers: 0101 0011 and 0111 0110.
To get to the answer, use the following method:

1. Starting at the right-hand side, the first sum is 1 + 0 = 1. Put 1 in the answer row below

2. Move to the next numbers to the left. The second sum is 1 + 1 = 10. Put 0 in the answer row below and carry 1 over to the next sum

3. Move to the next numbers to the left. There is a carry of 1, so ignore the top 0 and use the carry, so the third sum is 1 + 1 = 10. Put 0 in the answer row below and carry 1 over to the next sum

4. In the next sum to the left, ignore the top 0 again and use the carry, so the fourth sum is 1 + 0 = 1. Put 1 in the answer row below

5. In the next sum to the left there is no carry, so the fifth sum is 1 + 1 = 10. Put 0 in the answer row below and carry 1 over to the next sum

6. In the next sum to the left there is a carry of 1, ignore the top 0 and use the carry, so the sixth sum is 1 + 1 = 10. Put 0 in the answer row below and carry 1 over to the next sum

7. In the next sum to the left there is a carry of 1. This time, as the top number is a 1, it is used and not ignored like a 0, so the seventh sum is 1 + 1 + 1 = 11. Put 1 in the answer row below and carry 1 over to the next sum

8. In the last sum to the left, ignore the top 0 again and use the carry, so the final sum is 1 + 0 = 1. Put 1 in the answer row below

9. This gives us the answer of 11001001. We can check the answer by converting all three number back to denary and checking the sum is correct
Overflow errors
Sometimes, when adding two binary numbers we can end up with an extra digit that doesn’t fit. This is called an overflow error.
An explanation of binary overflow errors

This sum is fine as the original numbers have two digits, and the result of the sum also has two digits.

This sum has an overflow error. The original numbers had two binary digits, but the answer is three binary digits long.
The effects of an overflow error can vary. It might make the program crash or it might just ignore the extra digit on the left and produce an unexpected result (in this case, 2 + 3 = 0!).

Translation of Word Problems to Numerical Equations
There are two steps to solving math word problems:
- Translate the wording into a numeric equation that combines smaller “expressions”
- Solve the equation!
Suggestions:
- Read the problem entirely
Get a feel for the whole problem - List information and the variables you identify
Attach units of measure to the variables (gallons, miles, inches, etc.) - Define what answer you need,
as well as its units of measure - Work in an organized manner
Working clearly will help you think clearly- Draw and label all graphs and pictures clearly
- Note or explain each step of your process;
this will help you track variables and remember their meanings
- Look for the “key” words (above)
Certain words indicate certain mathematical operations:
Math expressions (examples):
after you review the keywords, test yourself
| addition: 5+x | subtraction: 5-x |
| multiplication: 5*x; 5x | division: 5 ÷ x; 5/x |
| Exercise: (“mouse over” the block for answer) | |
| Key words for addition + increased by; more than; combined together; total of; sum; added to |
|
| What is the sum of 8 and y? | 8 + y |
| Express the number (x) of apples increased by two |
x + 2 |
| Express the total weight of Alphie the dog (x) and Cyrus the cat (y) |
x + y |
| Key words for Subtraction – less than, fewer than, reduced by, decreased by, difference of |
|
| What is four less than y | y – 4 |
| What is nine less than a number (y) | y – 9 |
| What if the number (x) of pizzas was reduced by 6? |
x – 6 |
| What is the difference of my weight (x) and your weight (y) |
x – y |
| Key words for multiplication * x or integers next to each other (5y, xy): of, times, multiplied by |
|
| What is y multiplied by 13 | 13y or 13 * y |
| Three runners averaged “y” minutes. Express their total running time: |
3y |
| I drive my car at 55 miles per hour. How far will I go in “x” hours? |
55x |
| Key words for division ÷ / per, a; out of; ratio of, quotient of; percent (divide by 100) |
|
| What is the quotient of y and 3 | y/3 or y ÷ 3 |
| Three students rent an apartment for $ “x” /month. What will each have to pay? |
x/3 or x ÷ 3 |
| “y” items cost a total of $25.00. Express their average cost: |
25/y or 25 ÷ y |
More vocabulary and key words:
- “Per” means “divided by”
as “I drove 90 miles on three gallons of gas, so I got 30 miles per gallon.”
(Also 30 miles/gallon) - “a” sometimes means “divided by”
as in “When I filled up, I paid $10.50 for three gallons of gasoline,
so the gas was 3.50 a gallon, or $3.50/gallon - “less than”
If you need to translate “1.5 less than x”, the temptation is to write “1.5 – x”. DON’T! Put a “real world” situation in, and you’ll see how this is wrong: “He makes $1.50 an hour less than me.” You do NOT figure his wage by subtracting your wage from $1.50.
Instead, you subtract $1.50 from your wage - “quotient/ratio of” constructions
If a problems says “the ratio of x and y“,
it means “x divided by y” or x/y or x ÷ y - “difference between/of” constructions
If the problem says “the difference of x and y“,
it means “x – y“
| What if the number (x) of children was reduced by six, and then they had to share twenty dollars? How much would each get? | 20/(x – 6) |
| What is 9 more than y? | y + 9 |
| What is the ratio of 9 more than y to y? | (y + 9)/y |
| What is nine less than the total of a number (y) and two |
(y + 2) – 9 or y – 7 |
| The length of a football field is 30 yards more than its width “y”. Express the length of the field in terms of its width y | y + 30 |


